题目描述

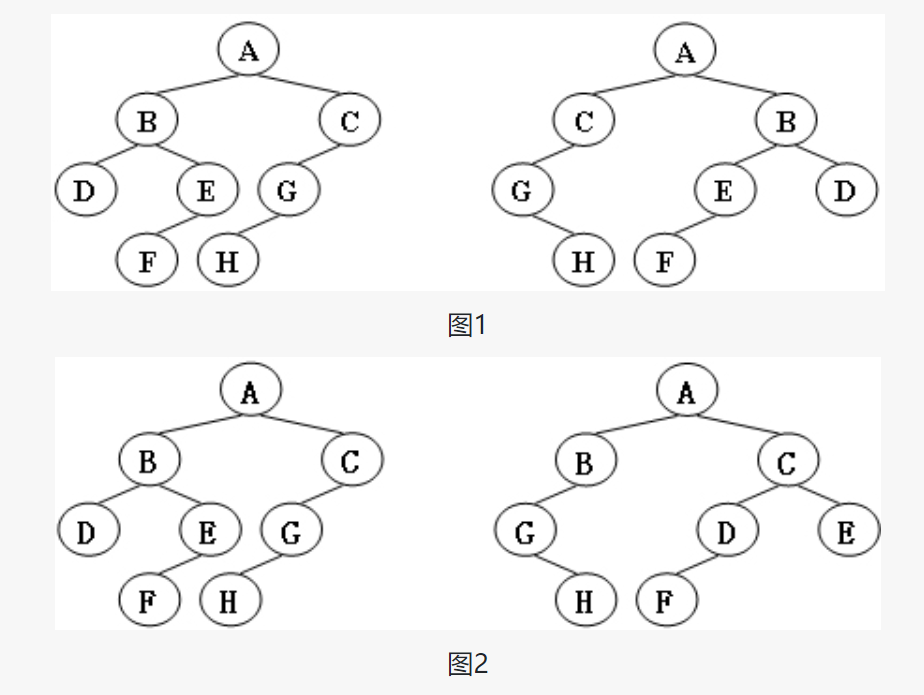
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

avatar

现给定两棵树，请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的，输出“Yes”，否则输出“No”。
输入样例1（对应图1）：
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2（对应图2）：
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No

分析

1.存储二叉树

  • 一般会使用链表来存储二叉树，但这里因为要等到所有的结点输入完毕后才能知道头结点是哪个(第一个样例第二组输入),所以这里使用链表不是很方便
  • 因此这里使用了静态链表的方式存储，也就是使用结构体数组，每个结构体是一个结点，其中包含数据域和两个指针域，指针域分别指向左孩子和右孩子在数组中的位置。
  • 也可以使用顺序表(数组)的方式存储二叉树，只需要将其看成是完全二叉树即可

    2.判断树是否同构

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    //判断两棵二叉树是否同构
    //now0为第一颗二叉树当前访问到的结点位置，now1为第二颗二叉树当前访问到的结点位置
    //每次调用equaltree，都可以把now0和now1所指向的结点看成一颗树的根节点
    int equaltree(int now0,int now1) {
    	if (now0 == -1 && now1 == -1)  //两个根节点都为空，两棵树同构
    		return 1;
    	if ((now0 == -1 && now1 != -1) || (now0 != -1 && now1 == -1)) //两个根节点一个为空一个不为空，不同构
    		return 0;
    	if (bintrees[0][now0].data != bintrees[1][now1].data) //两个根节点数据不同，不同构
    		return 0;
    	if ((bintrees[0][now0].lChildpos == -1) && (bintrees[1][now1].lChildpos == -1)) //左子树都为空，判断右子树是否同构即可
    		return equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].rChildpos);
    	//两棵左子树都存在并且根节点相同，这时如果同构的话一定是左子树之间同构，右子树之间同构
    	if ((bintrees[0][now0].lChildpos != -1) && (bintrees[1][now1].lChildpos != -1) && (bintrees[0][bintrees[0][now0].lChildpos].data == bintrees[1][bintrees[1][now1].lChildpos].data))
    		return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].lChildpos) && 
    			equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].rChildpos));
    	else //这时如果同构，只可能是第一棵二叉树的左子树和第二棵二叉树右子树同构，第一棵二叉树的右子树和第二棵二叉树左子树同构
    		return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].rChildpos) &&
    			equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].lChildpos));
    	/*
    	不对子树的根节点进行判断，替代最后的if else，但是效率很低
    	return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].lChildpos) &&equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].rChildpos)) 
    	|| (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].rChildpos) &&equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].lChildpos));
    		*/
    }
  • 这个函数的核心思想是每次调用equaltree，都可以把now0和now1所指向的结点看成一颗树的根节点
  • 在两个根节点相同的情况下，下一步要做的就是判断左子树和右子树是否匹配,如果最终两棵树同构的话只有两种可能:
    1. 左子树之间同构，右子树之间同构
    2. 左子树和右子树同构，右子树和左子树同构

基于以上两种可能，我们可以通过一个if提前预知是哪种可能:

1
2
3
4
5
6
7
//两棵左子树都存在并且根节点相同，这时如果同构的话一定是左子树之间同构，右子树之间同构
if ((bintrees[0][now0].lChildpos != -1) && (bintrees[1][now1].lChildpos != -1) && (bintrees[0][bintrees[0][now0].lChildpos].data == bintrees[1][bintrees[1][now1].lChildpos].data))
	return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].lChildpos) && 
		equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].rChildpos));
else //这时如果同构，只可能是第一棵二叉树的左子树和第二棵二叉树右子树同构，第一棵二叉树的右子树和第二棵二叉树左子树同构
	return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].rChildpos) &&
		equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].lChildpos));
  • 如果不提前判断是哪种可能的话，也可直接暴力匹配一遍，也就是直接把两种可能
    1
    2
    3
    //不对子树的根节点进行判断，替代最后的if else，效率很低
    return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].lChildpos) &&equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].rChildpos)) 
        || (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].rChildpos) &&equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].lChildpos));
    这样也能通过，只是时间从4ms变成了16ms

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<iostream>
using namespace std;

//二叉树结点
struct TreeNode {
	char data; //数据域，存放大写英文字母
	int lChildpos,rChildpos; //存储左孩子和有孩子的位置
};

struct TreeNode bintrees[2][20]; //使用静态链表存储二叉树

//构建二叉树
int buildTree(int i) {
	int n;
	char data, lChildpos, rChildpos;
	int checked[20] = { 0 };

	cin >> n;
	for (int j = 0; j < n; j++) {
		cin >> data >> lChildpos >> rChildpos;
		bintrees[i][j].data = data;
		if (lChildpos != '-') {
			bintrees[i][j].lChildpos = lChildpos - '0';
			checked[bintrees[i][j].lChildpos] = 1;
		}
		else
			bintrees[i][j].lChildpos = -1;
		if (rChildpos != '-') {
			bintrees[i][j].rChildpos = rChildpos - '0';
			checked[bintrees[i][j].rChildpos] = 1;
		}
		else
			bintrees[i][j].rChildpos = -1;
	}
	//找出没有人指向的结点，即为根节点
	for (int j = 0; j < n; j++) {
		if (checked[j] == 0)
			return j; //返回根节点在数组中的位置
	}
	return -1;
}

//判断两棵二叉树是否同构
//now0为第一颗二叉树当前访问到的结点位置，now1为第二颗二叉树当前访问到的结点位置
//每次调用equaltree，都可以把now0和now1所指向的结点看成一颗树的根节点
int equaltree(int now0,int now1) {
	if (now0 == -1 && now1 == -1)  //两个根节点都为空，两棵树同构
		return 1;
	if ((now0 == -1 && now1 != -1) || (now0 != -1 && now1 == -1)) //两个根节点一个为空一个不为空，不同构
		return 0;
	if (bintrees[0][now0].data != bintrees[1][now1].data) //两个根节点数据不同，不同构
		return 0;
	if ((bintrees[0][now0].lChildpos == -1) && (bintrees[1][now1].lChildpos == -1)) //左子树都为空，判断右子树是否同构即可
		return equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].rChildpos);
	//两棵左子树都存在并且根节点相同，这时如果同构的话一定是左子树之间同构，右子树之间同构
	if ((bintrees[0][now0].lChildpos != -1) && (bintrees[1][now1].lChildpos != -1) && (bintrees[0][bintrees[0][now0].lChildpos].data == bintrees[1][bintrees[1][now1].lChildpos].data))
		return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].lChildpos) && 
			equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].rChildpos));
	else //这时如果同构，只可能是第一棵二叉树的左子树和第二棵二叉树右子树同构，第一棵二叉树的右子树和第二棵二叉树左子树同构
		return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].rChildpos) &&
			equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].lChildpos));
	/*
	不对子树的根节点进行判断，替代最后的if else，但是效率很低
	return (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].lChildpos) &&equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].rChildpos)) 
	|| (equaltree(bintrees[0][now0].lChildpos, bintrees[1][now1].rChildpos) &&equaltree(bintrees[0][now0].rChildpos, bintrees[1][now1].lChildpos));
		*/
}

int main() {
	int root0, root1;

	root0 = buildTree(0);
	root1 = buildTree(1);
	if (equaltree(root0, root1))
		cout << "Yes" << endl;
	else
		cout << "No" << endl;
	return 0;
}