题目描述

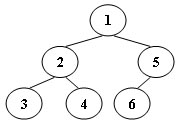
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

Figure 1

Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: “Push X” where X is the index of the node being pushed onto the stack; or “Pop” meaning to pop one node from the stack.

Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
Sample Output:
3 4 2 6 5 1

分析

  • 题目中给出的出栈序列是中序遍历，而入栈的序列是先序遍历的序列，要求的是后序遍历的序列
  • 根据树的重构的知识( https://blog.csdn.net/zhanw15/article/details/80619738 ),我们可以用先序遍历和中序遍历重构出整个二叉树，然后再进行后序遍历
  • 重构的思路：使用递归，用一个队列存储先序遍历，该队列的首元素即为中序遍历的根节点，然后在中序遍历啊中找到这个元素，该元素左边是它的左子树，右边是右子树

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<iostream>
#include<stack>
#include<vector>
#include<string>
#include<queue>

using namespace std;

int first = 1;
typedef struct TreeNode * position;

struct TreeNode {
	int number; //存储结点的序号
	position left,right;
};

stack<int> create_inorder; //用于模拟出栈入栈的过程，从的得到中序遍历的序列
vector<int> inorder; //存储中序遍历的序列
queue<int> preorder; //存储先序便利的序列，用队列存储，首元素为当前根结点

int findroot(int number) { //在中序遍历的序列中找到当前根节点的位置
	for (int i = 0; i < inorder.size(); i++) {
		if (inorder[i] == number)
			return i;
	}
}

//根据中序遍历和先序遍历的序列重构二叉树
position createBinTree(int left,int right) {
	if (left > right)
		return NULL;
	int root,rootpos;
	//struct TreeNode node;
	position nodepos = new TreeNode;
	
	root = preorder.front();
	preorder.pop();
	rootpos = findroot(root);
	nodepos->number = root;
	//cout << rootpos << endl;
	nodepos->left = createBinTree(left, rootpos - 1);
	nodepos->right = createBinTree(rootpos + 1, right);
	return nodepos;
}

//后序遍历二叉树
void postTraverse(struct TreeNode root) {
	if (root.left != NULL)
		postTraverse(*root.left);
	if (root.right != NULL)
		postTraverse(*root.right);
	if (!first) 
		cout << ' ';	
	first = 0;
	cout << root.number;
	return;
}

int main() {
	int N,number;
	string input;
	position root;

	cin >> N;
	for (int i = 0; i < 2 * N; i++) {
		cin >> input;
		if (!input.compare("Push")) {
			cin >> number;
			create_inorder.push(number);
			preorder.push(number);
		}
		else {
			inorder.push_back(create_inorder.top());
			create_inorder.pop();
		}
	}
	root = createBinTree(0,N-1);
	postTraverse(*root);
	return 0;
}