Here are some notes on learning this algorithm, to practice my English writing skills I write them in English.

This algorithm is not a fixed point iteration method, actually it is a symbolic execution technique rather than a dataflow analysis approach. So it took me a lot of time to understand it.

The Pseudocode of this algorithm is in CS 426 Topic 5: SSA and the SSA Construction Algorithm. It closely resembles the algorithm described in the original paper Constant Propagation with Conditional Branches.

Here are some of the questions I have pondered:

What are the meanings of FlowWL and SSAWL?

FlowWL simply adds all SSA edges to SSAWL, and that’s why every flow edge within it is only be executed once.

SSAWL means updating the constant information once a change is detected in a variable’s lattice. Due to the properties of SSA , there is no need for two separate product lattices(INPUT and OUTPUT) for each instruction. Instead, we only require a single lattice for each variable.

When dealing with unexecuted flow edges, why does this algorithm only invoke VisitInst(E->sink) during the initial visit to E->sink via flow edges, whereas it calls VisitPhi(φ) ∀ φ ∈ E->sink every time?

considering such a situation:

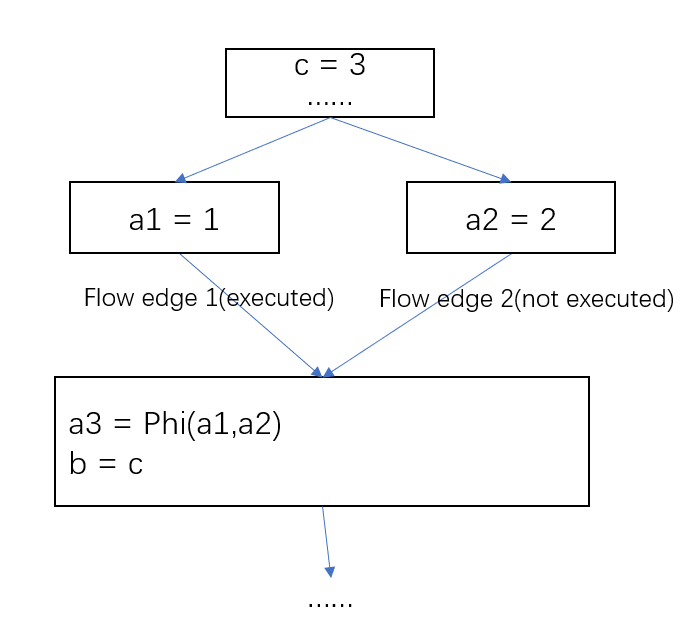
When this algorithm handles flow edge 2, there is no need to reconsider b = c again since it is impossible to observe any new changes(This is ensured by the feature of SSA). However, a3 = phi(a1, a2) needs to be reevaluated because of the impact of a2.

Why this algorithm need this statement?

One thing that needs to be noted is that the algorithm presented in this slide assumes that every basic block has only one instruction for convenience, which implies that all instructions, except for conditional branches, behave as if they were unconditional branches. This statement fetches the next instruction in the case of all instructions except conditional branches.

However, if this algorithm is designed to work in typical situations, it can be replaced by an iteration over the instructions within a basic block and a special process of unconditional branches in visitInst.

Actually the original paper does not explicitly mention “basic blocks”. Instead, it discusses a flow graph consisting of individual statements. This topic is further explained in section 12.6 of the book Advanced Compiler Design and Implementation.